What are metaheuristics?
The term heuristics describes a procedure by which a probable and practicable solution to a problem can be found with limited knowledge and time restrictions.
Heuristic methods, which are often used by the owners of electronic devices, are ‘trial and error’ and the exclusion method. The latter is also one of the specialties of Sherlock Holmes:
“When you have excluded the impossible, whatever remains, however improbable, must be the truth.” – The Adventure of the Beryl Coronet / Sherlock Holmes
The ‘meta’ in metaheuristics describes, that this is a higher level of heuristics, which – at least theoretically – can be applied to any problem: Be it a chess problem or the batch formation in a distribution center.
In the article ‘Metaheuristics in Combinatorial Optimization: Overview and Conceptual Comparison‘ the properties of metaheuristics are described as follows:
- Metaheuristics are strategies, which ‘steer’ the search process
- The goal is to efficiently explore the search space to find suitable solutions
- Techniques that include metaheuristic algorithms range from simple local search methods to complex learning processes
- Metaheuristic algorithms are approximate and usually non-deterministic
- They may contain mechanisms to avoid being trapped in limited areas of the search space
- The basic concepts of metaheuristics allow a description on an abstract level
- Metaheuristics are not problem specific
- Metaheuristics can use domain knowledge (e.g. from the field of intralogistics) in the form of more specialized heuristics, which are controlled by a strategy located above it
To get back to detective work: A metaheuristic Sherlock would identify as many people as possible in a short period of time, who are also criminals with a relatively high probability, by going for a walk and using his analytical skills to look for relevant data points. But this is not a wise use of a Sherlock Holmes’ time, if police patrols can be used for the problem.
The field of metaheuristics includes many methods and procedures, not all of which can be discussed in this paper. However, the following diagram should at least give a first overview.
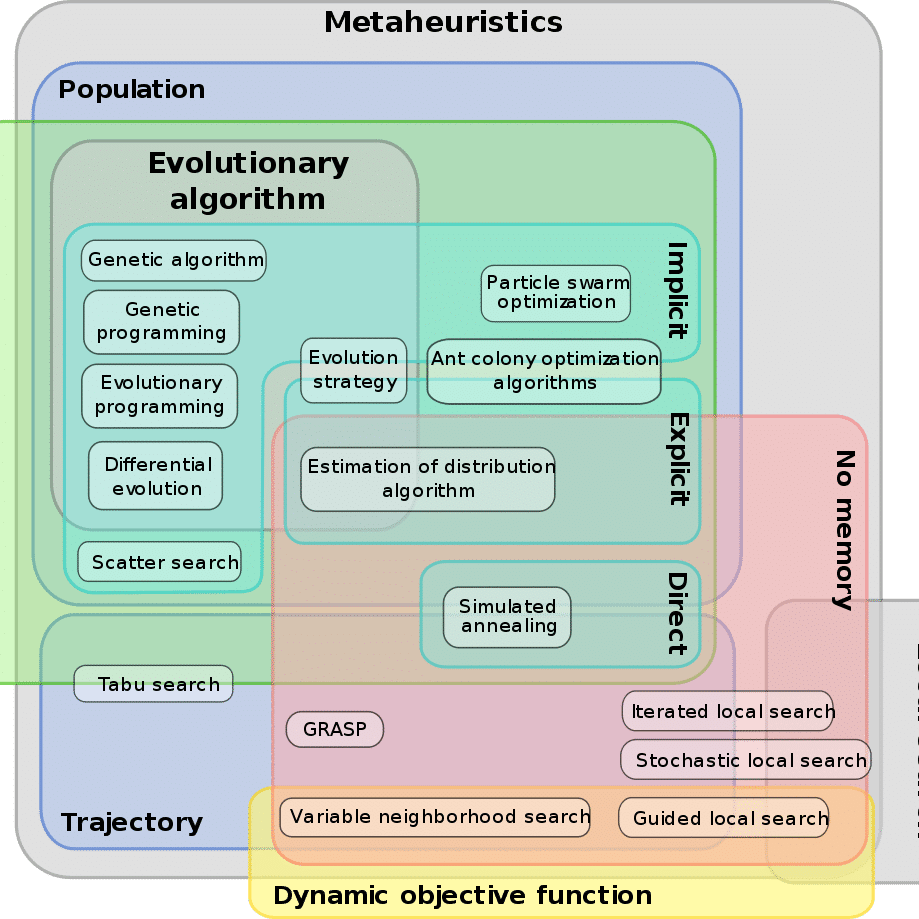
In intralogistics, the scarcity of time and computing power resources is a linchpin of all optimization processes: More and more small orders have to pass through the path from goods receipt to dispatch as quickly as possible. As a result, it is often not possible to find the optimal solution, but finding an optimized one is. This challenge is also described by the seven Rs of logistics:
- The right product
- in the right condition
- at the right time
- to the right recipient
- in the right quantity
- with the right information
- with the right costs
The need for large, high-quality data sets to optimize metaheuristics
In the field of research, real data is often not used, but scenarios are modeled that use an idealized warehouse layout – which is also due to the fact that companies rarely grant access to this data. The scenarios of the logistics industry are much more complex compared to the experimental layouts used in research. For example, the paper “An efficient hybrid algorithm for integrated order batching, sequencing and routing problem” by Chen, T.-L. et al, published in 2015, deals with a warehouse with twelve shelves, each with space for one item, which must take into account a maximum of eight orders with a maximum of ten items. In contrast, a modern distribution center often has space for more than 100,000 storage locations, which can result in batch formations of 5,000 to 10,000 items.
Metaheuristics that quickly arrive at satisfactory solutions in small scenarios can fail in complex ones. Therefore it is important to work with the large volumes of data in the highest possible quality.

Solver, heuristics and conditions
The road to success in order to find the most efficient solution lies in the precise and individual definition of the conditions of the business processes: Which aspect should be optimized? What are the limits and boundary conditions of optimization and how many resources are available until an improvement has to be achieved?
In manual warehouses with dynamic storage, for example, the walking distances should be minimized by keeping the number of aisle changes as low as possible. In order to achieve this successfully, the constraints must be precisely defined: What is the maximum size of a batch? What is the maximum item quantity of a particular type or the maximum quantity of individual orders? The solver is the program that applies one or more (meta-)heuristics or algorithms, taking into account the conditions, to achieve an approximation to a defined goal.
The difference between heuristics and algorithms
An algorithm describes a systematic, logical rule or procedure, which leads to the solution of an existing problem. In contrast to this there is the faster, but also more error-prone heuristic.
Stangl, W. (2020). Stichwort: ‘Algorithmus’. Online Lexikon für Psychologie und Pädagogik.
Probability as optimization engine
While an algorithm runs through a logical chain, which can be very long and resource intensive because of this, a heuristic runs through many small cycles, which can be computed faster and which are kept running by probabilities in the following example.
In the case of the mentioned ‘Simulated Annealing’ an improvement is always accepted and the cycle is run through again. In contrast, a deterioration is only accepted with a certain probability. Thus, a global maximum or minimum can be quickly identified, since the start solution is always the end value of a previous cycle. The term ‘annealing’ here is borrowed from the process known as ‘annealing’, in which a material is first heated, then held at a certain temperature and shaped, and finally cooled. The controlled heating and cooling ensures that the material is as close as possible to the desired strength value. Simulated annealing’ uses a global minimum or maximum value to aim for a solution. With this link to an archived page solutions for the traveling salesman problem can be achieved with a temperature maximum as well as a temperature minimum.
In intralogistics, one of the standard problems is that of the traveling salesman who wants to choose the most efficient route for his sales tour. In this example, ‘Simulated Annealing’ is used to find a route that connects all 125 points without having to travel to the same point twice.
This diagram shows the process behind the animated image.
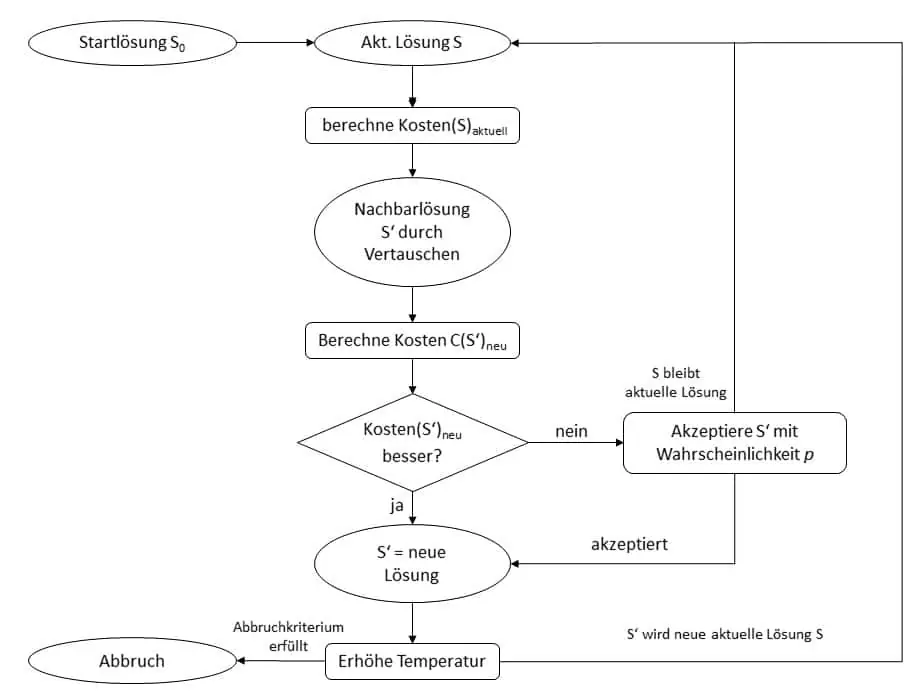
In the case of a new problem, test runs are first used to determine a suitable procedure for finding a good starting solution, as well as a suitable parameter β, which influences how fast the heating occurs in this case. A too rapid heating reduces the search space too much, a too slow heating can lead to the possibility to leave global optima again.
The structural design for use in intralogistics
To apply such a solver construct, the following building blocks are required.
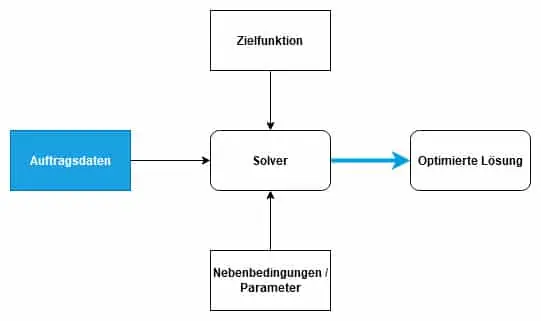
The solver itself is the central, but not the critical element. A value-adding solution can only be found if the order data is available in sufficient quantity and quality and if the auxiliary conditions and parameters have been individually adapted to the intralogistic business processes of the respective warehouse. Otherwise, the classic problem of every optimization process applies: “Garbage in, garbage out”. The correct application of the intralogistic domain knowledge at the level of strategy, parameters and data is the prerequisite for an efficient solver configuration.
The test scenario must be transparent for both sides
The mathematics behind it can often be found in publicly accessible sources, but the key is the individual adaptation and parameterization, which the project partners work out collaboratively at eye level. After all, distribution centers are complex systems in which human beings can often only recognize optimization potential and current operating states with the help of machine processing.
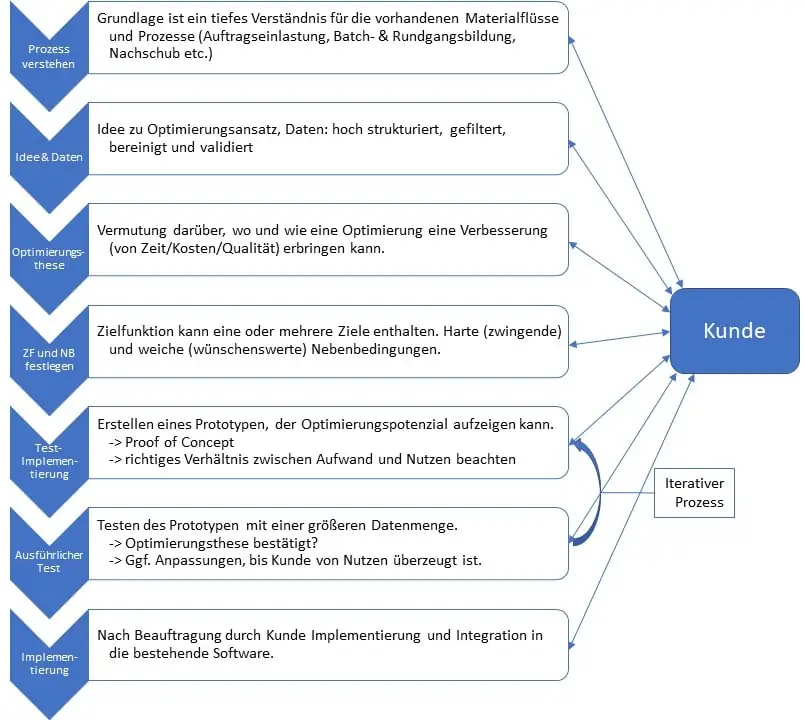
Joint iterative development ensures that the parameters target condition, job data and constraints have the highest possible quality. Depending on the solver used, different solutions can be created at different speeds. Standardized solutions quickly reach their limits due to the lack of adaptability.
Individual situation and process based solver machines
The key to fast and optimized results are therefore solvers that are adapted to the different processes and situations in the warehouse. Depending on the method used, different results can be achieved under the same conditions. For example, batch formation can be done by one solver, but the route planning of the picker can be done by another one to ensure that the results are as fast and of as high quality as possible through individual adaptation without requiring a lot of computing time or power. Situation-based solver solutions for full and partial load are also conceivable, since special conditions prevail here as well, which may not be solved sufficiently by a standardized solution.
Summary
Metaheuristics are an excellent tool for optimizing intralogistic processes. But they can only work if the order data is available in high quality and the parameters are individually adapted to the situation and the business processes. The best possible effectiveness of these solvers can only be achieved if communication between the project partners is at eye level and transparent and if test implementations are run with real, high-quality data.